הוכחות אפס-ידע שהוסברו חלק 2: הוכחות לא-אינטראקטיביות שאינן אינטראקטיביות

בחלק 1 של סדרת הוכחת אפס הידע שלנו, הסברנו כיצד הוכחת ידע אפס יכולה לעבוד כאשר האמת והפרוביור מתקשרים זה עם זה..

הוכחת אינטראקטיבית עם אפס-אינטראקציה היא היתרון שרק המאמת יכול להיות משוכנע לחלוטין שלפרובר יש את הידע. אבל זה יכול להיות גם חיסרון.

אם עוברי אורח ומשקיפים לא יכולים לאמת את התביעה, התובע צריך לקיים אינטראקציה עם כל מאמת באופן עצמאי – מה שלוקח זמן והוא עתיר משאבים.

בזה, חלק 2, נסקור הוכחות לא-אינטראקטיביות שאינן אינטראקטיביות.

הוכחות אפס-אינטראקטיביות שאינן אינטראקטיביות

הסיבה להוכחות אפס-אינטראקטיביות שאינן אינטראקטיביות היא לאפשר למספר גדול של צופים לאמת את ההוכחה בצורה יעילה.

אנחנו לא תמיד צריכים להפוך הוכחות לאפס אינטראקטיביות. לעתים קרובות מספיק ניתן למצוא מאמת מהימן, אשר מתחייב לשלמות ההוכחה.

דוגמה להוכחות אפס-אינטראקטיביות שאינן אינטראקטיביות: סודוקו וקלפי משחק

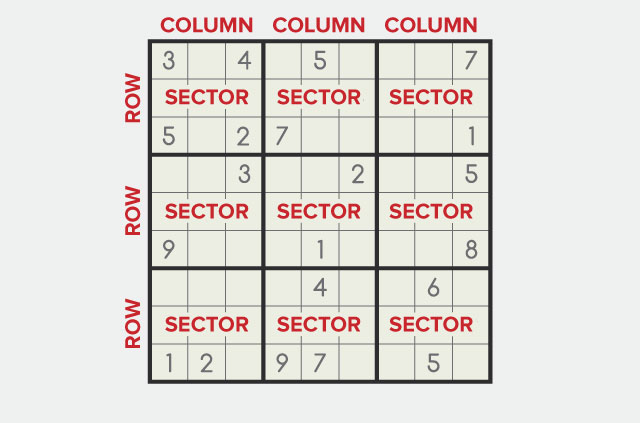
סודוקו הוא משחק בקושי משתנה אך כללים פשוטים יחסית. כל אחת מ -9 השורות, 9 העמודות ו -9 המגזרים (כפי שצוין על ידי הקו השחור העבה) חייבת להכיל כל מספר בין 1 ל -9 בדיוק פעם אחת.

תאר לעצמך שהפתרון לפאזל סודוקו קשה במיוחד להשגה, ולוקח ימים אפילו למחשב-על לחשב אותו..

אבל מישהו (המעיל) טוען שיש לו את הפיתרון לפאזל ומוכן למכור אותו במחיר. כיצד הם יכולים להוכיח שיש להם את הפיתרון – מבלי לחשוף אותו – כך שהמאמת מוכן לבצע תשלום?

ההוכחה:

הפרובר צריך 27 קלפי משחק (מכל חליפה) שמספרם 1-9–243 בסך הכל.

כעת, הפרוזר מכניס שלושה קלפים עם המספר המתאים לפיתרון סודוקו הנכון בכל קופסא. E.G., אם התשובה הנכונה עבור התיבה היא 7, התובע יניח 3 קלפי משחק עם הערך של 7 בתוכה.

על שולחן סודוקו ניתן לראות כמה תשובות. על תיבות אלה, ענו, הקלפים משחקים עם פנים כלפי מעלה. על תיבות סודוקו הריקות מונחים את הקלפים פנים למטה.

כדי להוכיח שהקלפים עם הפנים כלפי מטה כולם נמצאים במצב הנכון (מבלי לחשוף את הפיתרון), על התובע:

• קח את הכרטיס העליון מכל שורה ולעשות 9 ערימות
• קח את הכרטיס העליון מכל טור ולעשות 9 ערימות
• קח את הקלפים שנותרו מכל מגזר ולעשות 9 ערימות

לאחר מכן כל ערימה מדשדשת ומסתובבת.

כל מספר בין 1-9 חייב להופיע בכל שורה, טור וסקטור סודוקו. כך שאם כל ערימה מכרטיסי ה- prover (מערימות השורה, העמודה והמגזר) מכילה כל קלף משחק המוערך 1-9, אנו יודעים שהם חייבים לקבל את הפיתרון.

יישומים להוכחות אפס-ידע

יש להודות, התחום הצעיר יחסית של הוכחות להכרת אפס טרם מצא את ההשלמה שאולי מגיע לה. עם זאת הם עשויים להתגלות כבעלי ערך רב.

בעיות מתמטיות רבות דומות לפאזל סודוקו (לדוגמא בעיית צביעה גרפית). אם נוכל להשתמש בעקרון שלמעלה ולהחיל אותו בהצלחה על מגוון בעיות, ייתכן שנוכל להשתמש ולסחור במשאבי חישוב ובעיות מתמטיות בצורה יעילה יותר. או אולי לפתור מהרשמות מתמטיות במהירות.

קודוס לרונן גראדווהל, מוני נאור, בני פנקס וגיא רוטבלום