Bukti pengetahuan yang kurang jelas dijelaskan Bahagian 2: Keterangan pengetahuan sifar tidak interaktif

Dalam bahagian 1 siri bukti pengetahuan sifar kami, kami menerangkan bagaimana bukti pengetahuan sifar dapat berfungsi apabila pengesah dan prover itu berinteraksi antara satu sama lain.

Bukti pengetahuan sifar interaktif mempunyai kelebihan yang hanya pengesah dapat benar-benar yakin bahawa prover mempunyai pengetahuan. Tetapi ini juga boleh merugikan.

Sekiranya pengamat dan pemerhati tidak boleh mengesahkan tuntutan tersebut, prover kemudiannya harus berinteraksi dengan setiap pengesah secara bebas-yang memerlukan masa dan sumber intensif.

Dalam hal ini, bahagian 2 kita akan melihat bukti pengetahuan sifar yang tidak interaktif.

Pembuktian pengetahuan sifar bukan interaktif

Sebab-sebab keterangan pengetahuan sifar bukan interaktif adalah untuk membolehkan sejumlah besar pemerhati mengesahkan bukti dengan cekap.

Kami tidak semestinya perlu membuat bukti sifar pengetahuan yang tidak bersifat interaktif. Selalunya cukup mungkin untuk mencari pengesahan yang dipercayai, yang menjamin integriti bukti.

Contoh bukti pengetahuan sifar tidak interaktif: Sudoku dan kad bermain

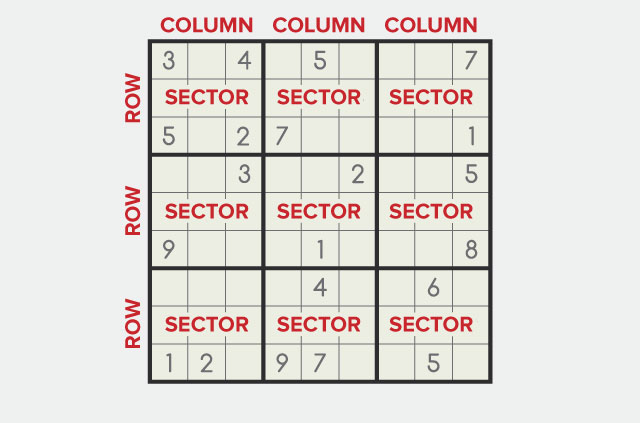
Sudoku adalah permainan dengan kesukaran yang berbeza-beza tetapi kaedah yang agak mudah. Setiap daripada 9 baris, 9 tiang, dan 9 sektor (seperti yang ditunjukkan oleh garis hitam tebal) mesti mengandungi setiap nombor dari 1 hingga 9 tepat sekali.

Bayangkan bahawa penyelesaian kepada teka-teki sudoku sangat sukar diperoleh, dan memerlukan waktu beberapa hari untuk dikomputerkan.

Tetapi seseorang (prover) mendakwa mempunyai penyelesaian kepada teka-teki dan sanggup menjualnya untuk harga. Bagaimanakah mereka boleh membuktikan mereka mempunyai penyelesaian-tanpa mendedahkannya-jadi pengesah bersedia untuk membuat pembayaran?

Bukti:

Prover memerlukan 27 bermain kad (dari mana-mana guaman) berjumlah 1-9-243 secara total.

Sekarang, prover meletakkan tiga kad dengan nombor yang sepadan dengan penyelesaian Sudoku yang betul di setiap kotak. E.G., jika jawapan yang betul untuk kotak adalah 7, prover akan meletakkan 3 kad bermain dengan nilai 7 di dalamnya.

Pada jadual Sudoku, beberapa jawapan akan dapat dilihat. Pada kotak-kotak ini, kad-kad yang dipanggil diletakkan menghadapi. Pada kotak Sudoku yang kosong, kad diletakkan menghadap ke bawah.

Untuk membuktikan kad pendengaran berada di kedudukan yang betul (tanpa mendedahkan penyelesaiannya), prover mesti:

• Ambil kad teratas dari setiap baris dan buat 9 buasir
• Ambil kad teratas dari setiap ruangan dan buat 9 buasir
• Ambil baki kad dari setiap sektor dan buat 9 buasir

Setiap longgokan kemudian digerakkan dan berbalik.

Setiap nombor antara 1-9 mesti muncul di setiap baris, lajur, dan sektor Sudoku. Jadi jika setiap timbunan kad prover (dari baris, lajur, dan timbunan sektor) mengandungi setiap kad bermain bernilai 1-9, kita tahu bahawa mereka mesti mempunyai penyelesaian.

Aplikasi untuk bukti Zero-pengetahuan

Diakui, bidang yang agak muda bukti bukti sifar masih belum dapat diterima penerimaannya. Walau bagaimanapun, mereka mungkin terbukti sangat berharga.

Banyak masalah matematik sama dengan teka-teki Sudoku (contohnya masalah Warna Pewarna). Sekiranya kita boleh menggunakan prinsip di atas dan berjaya menerapkannya kepada pelbagai masalah, kita mungkin dapat menggunakan dan memperdagangkan sumber-sumber perhitungan dan masalah matematik dengan lebih cekap. Atau mungkin menyelesaikan quandaries matematik dengan lebih cepat.

Kudos kepada Ronen Gradwohl, Moni Naor, Benny Pinkas, dan Guy Rothblum